Dit onderwerp bevat 41 reacties, 10 deelnemers, en is laatst geüpdatet op 10 jaren, 3 maanden geleden door 
-
Berichten
-
Ben misschien en beetje dom (was in ieder geval niet sterk in wiskunde) , maar ik begrijp de sprong niet. De wortel 2 kwam min of meer bovendrijven. Kan iemand het even voor mij tekenen ? (serieus bedoeld).
Code:|\
| \c
| \ wortel 2 = 1.414
|a \
|1 \
|__b__\
1(Gelijkzijdige driehoek, 90, 45, 45 graden)
a kwadraat + b kwadraat = c kwadraat
altjid handig om te weten weet alleen niet hoe ik ze er groter en leesbaar op krijg iemand een idee werk met photobucket dom oke maar ben ook maar lasser pijpfitter van beroep
gr ruiterMijn langste boor was net te kort voor de keldermuur van 90cm dik, de muren worden naar boven toe wat dunner. Ik heb het opgelost zoals dat heel vroeger ging, een lange beitel draaien en kloppen. Zo’n lange beitel had ik niet, maar wel een aardpen van een meter. Met een griptang erop voor het draaien en wat flinke klappen was het zo gebeurd.
hier komt de “beitel” de muur uit.
wimb
hai wannox mooi gedaan maar
hiervoor is vrij eenvoudig een stukje gereedschap te maken
men neme een stuk draadstang van bv 16 mm
een draadstang verlenger van 16 mm
men boort in de zijkant van de verlenger een gat en tap daar 6 of 8 mm draad in
nu boort men een gat van de juiste diameter in een eind van de draadstang verlenger
boor vast zetten en je kunt een meter diep boren
nog sneller las gewoon een boor aan een draadstang van een meter wil je dieper draadstang verlenger er tussen en weer een meter
gr ruiterBonjour,
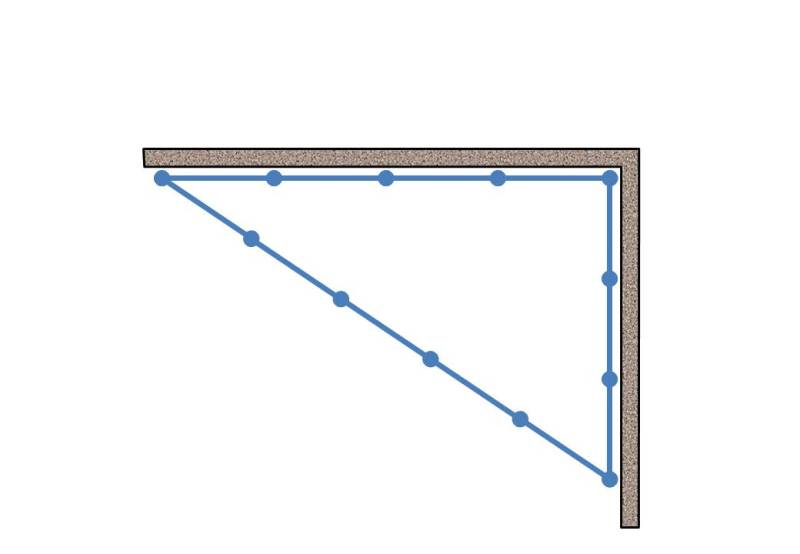
Om nog even op de goede oude Pythagoras terug te komen, op basis van zijn bekende wet kan met minimale middelen snel worden gecontroleerd of een hoek haaks is. U verdeelt daartoe een willekeurig stuk touw in 12 gelijke afstanden door er knopen in te leggen. Met dat touw kunt u dan de haaksheid van elke willekeurige hoek nagaan door toepassing van de 3-4-5 regel. Immers, 3kwadraat plus 4kwadraat is 5kwadraat, dus dit is een bijzonder geval van de rechthoekige driehoek waarbij de lengte van alle zijden een geheel getal is. Zie het plaatje hieronder.
De Romeinen deden het al op deze manier, maar zelfs in de tegenwoordige tijd kan deze truuk nog handig zijn. Bijvoorbeeld bij het uitzetten van grote oppervlakken of lengtes waar een standaard schrijfhaak of blokhaak gewoon veel te klein is. Denk hierbij aan zaken als omheiningen of terrassen, of het nagaan of de muren van een groot vertrek wel haaks op elkaar staan (in oude FR huizen dus meestal niet 🙁 ).
Ik vind het zelf erg handig altijd een dergelijk stuk touw met knopen te hebben liggen. Laatst nog gebruikt om te controleren of mijn dakvlakken een beetje haaks op het gevelvlak stonden. Nou, niet dus.
Salutations, Jos
Nog een wiskundige truc, bijna zo mooi als de door Jos beschreven Pythagoras-reeks 3-4-5, maar nu gebaseerd op het getal pi, de quotiënt tussen omvang (perimeter, vandaar het getal pi) en diameter van een cirkel. Werd door de oude Egyptenaren reeds meer dan duizend jaar voor Christus gebruikt.
Als men in een pijpleiding een haakse bocht wil maken kan men die zo aftekenen:
– Eerst het punt A aftekenen waar de andere ‘poot’ van de leiding moet komen
– dan eenmaal de radius naar binnen, en een half maal naar buiten aftekenen.
– dan kan men het stuk tussen de markeringen warm maken en buigen.
Dit berust op het gegeven dat een kwartboog een lengte van 0,5 maal pi heeft. Pi is gelijk 3.14, een half pi dus 1.57. De tweede decimale van pi vergeet men gewoon, en zegt:
“Einmal den Radius zum Maß, einmal den Radius vom Maß”.
Zo hoorde ik het tenminste van de pijplegger/lasser bij wie ik in mijn studietijd eens op een vakantiejob als hulpje gewerkt heb.Quote:Quote uit JP op 19/04/2014 10:57
Is de nummer 1 een niveau, waterpas voor blinden of slechtzienden ? Eventueel voor kleurenblinden ?
Ik merk overigens op dat de hellingshoek van de afvoer veel meer lijkt te bedragen dan de 1 cm per meter, waarvan men zegt dat dat de goede helling is om vloeibaar en meer solide fijn te laten glijden…Hier wil ik toch even serieus op ingaan.
Meer dan 1% helling is inderdaad niet aan te raden vanwege de scheiding van vloeistoffen en vaste stoffen die dan plaatsvindt. Hier heeft JP gelijk.
Maar mijn regenwaterpijp (1) heb ik alleen provisorisch op het putje P aangesloten; de definitieve aansluiting (2) ligt 8m verderop, dus dan werd het ongeveer 1%.
Zo vloeit uit een Bavards-gereedschap toch weer een serieuze discussie vort!
Om weer even een serieuze bijdrage te leveren en met het oog op dichtslibbende ateliers vol met gereedschap dat je toch niet meer gebruikt, wijs ik op een stichting [http://geredgereedschap.nl/], die er anderen graag gebruik van laat maken. Ik ken geen stichtingen of andere organisaties in LdF. Lokaal wordt hier wel regelmatig ingezameld voor projecten in Afrika. Ik deed een tijdje geleden afstand van een aantal schaven, die mijn grootvader in de jaren dertig aanschafte. Bij mij sinds 1962 eigenlijk als aandenken in de werkplaats, maar heb zo nooit gebruikt. Ik vind het een mooi idee dat ze nu zijn meegenomen door iemand uit het dorp, die met een aanhanger vol bruikbaar spul op pad is gegaan en dat – zonder strijkstok-gedoe- heeft afgeleverd. De betreffende persoon heeft ook veel tractoronderdelen bij zich en besteed 3 weken van zijn vakantie aan het repareren van oude beestjes ter plekke. Hulde dus aan dit soort mensen !
De nederlandse link naar de Easyscribe werkt niet meer.
Bij Amazone in Duitsland is deze nog wel te bestellen. Is hier goedkoper dan bij de franse variant.Wim3
Wim3,
bij deze gelegenheid nog eens de hele draad doorgelopen en een stomme fout in mijn bijdrage van 20-04 13:20 ontdekt.
De uitspraak van de pijplegger/lasser moet natuurlijk zijn:
“Einmal den Radius zum Maß, einhalbmal den Radius vom Maß”.De nederlandse link naar de Easyscribe werkt weer
Je moet ingelogd zijn om een antwoord op dit onderwerp te kunnen geven.
